A quick glance at Lambda And basic category theory

1 Categories

Category Theory คือสาขาคณิตศาสตร์ที่มีการประยุกต์ใช้อย่างกว้างขวางในวิทยาการคอมพิวเตอร์เชิงทฤษฎี แนวคิดต่างๆ เช่น Category, Functor, Monad, และอื่นๆ ซึ่งเดิมทีถูกนิยามใน Category Theory ได้กลายเป็นสิ่งสำคัญในการเข้าใจภาษาการเขียนโปรแกรมเชิงฟังก์ชัน (Functional Programming หรือ FP) และพาราดิกม์ต่างๆ

Category คือการขยายแนวคิดของ Set of Objects แบบคลาสสิก Category C ประกอบด้วยสิ่งที่เรียกว่า สามเอนทิตีทางคณิตศาสตร์:

1. class ob(C), ซึ่งองค์ประกอบของมันเรียกว่า Objects นักพัฒนาแบบ object-oriented คงจะเห็นว่านี่เป็นวิธีที่ดีในการเริ่มต้นการนิยาม

category ของ types คือ int, bool, char เป็นต้น ในการเขียนโปรแกรมเรามี category ที่น่าสนใจมากมาย และในหนังสือเล่มนี้ เราจะสำรวจบางอัน

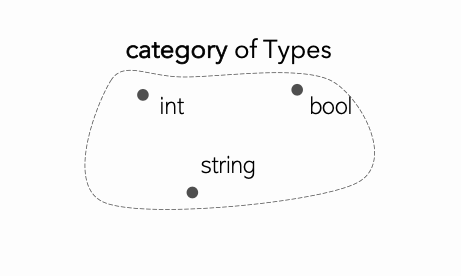
2. Collection ของ elements ที่เรียกว่า morphisms หรือ arrows แต่ละ morphism f มี source object a, และ target object b

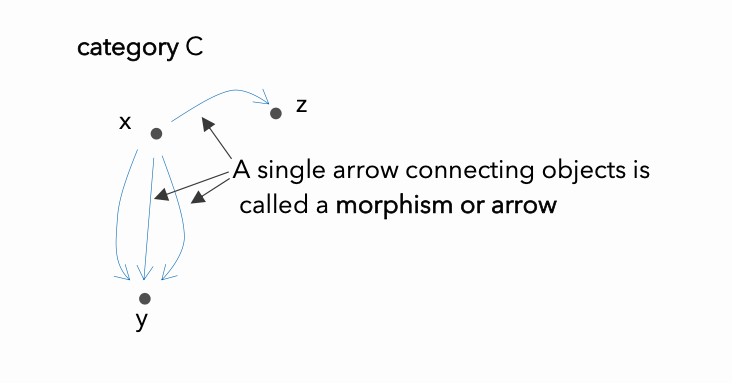
ลูกศรที่เชื่อมโยงระหว่าง Objects เรียกว่า morphism หรือ arrow

ใน Type category ของเรา, arrow ใดๆ จาก number ไปเป็น boolean เช่น จะเป็น function number → boolean ตัวอย่างบางตัวอาจจะเป็น:

var isEven = a => a % 2 === 0;

หรืออันนี้:

var isLessThan10 = a => a < 10;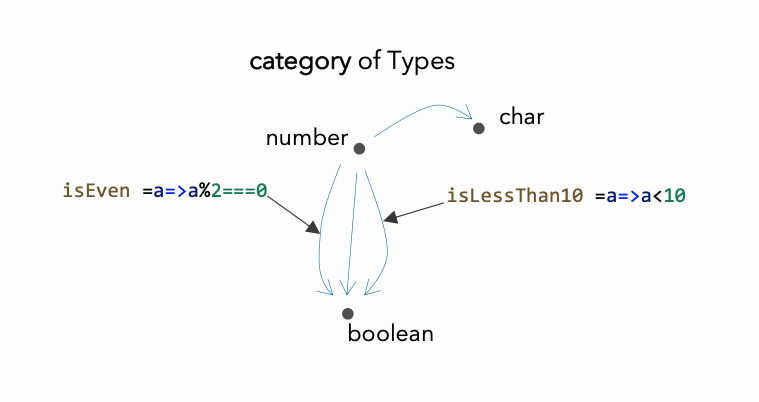

Focus พื้นฐานของ Category Theory คือ relations ระหว่าง Objects และไม่ใช่ Objects นั้นๆ เช่นเดียวกับ Set theory ที่เน้นที่เซ็ตของ Objects, functional developer ได้ยอมรับมุมมองที่แตกต่างนี้จาก Category Theory